Covariance Matrix Estimators Analysis
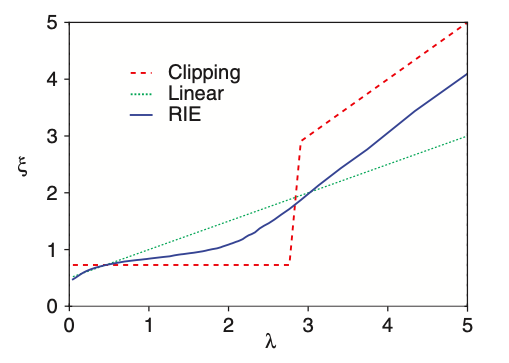
Comparison of the optimal shrinkage function that maps the empirical eigenvalue $\lambda_i$ onto ‘cleaned’ version, $\xi_i$
Formula

The question of building reliable estimators of covariance or of correlation matrices has a long history in finance, and more generally in multivariate statistical analysis. The performance of any mean-variance optimization scheme closely depends on the variance-covariance matrices. Therefore, it is of utmost importance to select a suitable metric against which candidate methods of covariance matrix estimators can be tested. In this section, I compare three commonly used covariance matrix estimators – the empirical covariance, the “eigenvalue clipping” covariance estimator, and the “optimal shrinkage” estimator by the out-of-sample volatility of the Markowitz portfolios built from each estimator.